Mit Zirkel und Lineal ein (fast) korrektes Quadrat aus einem Kreis ableiten
Die Quadratur des Kreises mit hoher Genauigkeit auf einfache Weise lösen
Lange Zeit war es niemand vergönnt, nur mithilfe von Zirkel und Lineal ein flächengleiches Quadrat aus einem gegebenen Kreis mit ausreichender Genauigkeit abzuleiten beziehungsweise zu konstruieren. Geistesblitze von Eduard Gregori beziehungsweise Heinrich Hemme, aber auch von Hans Hampl erlauben es heute jedoch, dieses Problem mit einer erstaunlichen Genauigkeit auf sehr einfache Weise zu lösen.
Insidern ist Hans Hampl schon lange als Schöpfer einer alternativen Sicht auf die Himmelscheibe von Nebra bekannt. Der ehemalige Grafiker hat umfangreiches Material erarbeitet, das den Blick auf dieses jahrtausendealte Artefakt in eine neue Richtung führte: Er hat auf der Grundlage seiner umfangreichen Berechnungen die These aufgestellt, die Himmelscheibe sei ein Teil einer astronomischen Uhr gewesen. Zum Beweis baute er mit damals üblichen Materialien das Modell einer Sternen-Rechenmaschine nach, um seine These zu untermauern.
Dabei nutzte er die damals üblichen Längenmaße, um seinen Nachbau funktionstüchtig erstellen zu können. Diese über Jahre sich hinziehenden Arbeiten hatten zur Folge, dass er eine Lösung fand, nur mit zeichnerischen Mitteln aus einem gegebenen Kreis ein (fast) flächengleiches Quadrat zu zeichnen. Mit mathematischen Mitteln ist diese Aufgabe sehr einfach zu lösen, zeichnerisch jedoch nicht.
Es ergibt sich eine Strecke von 62,03588 Millimeter für das Quadrat. Somit ist es rechnerisch problemlos möglich, einen Kreis sowie ein Quadrat mit gleichem Flächeninhalt zu errechnen und beispielsweise mit BeckerCAD zu zeichnen. Die dort vorhandene Flächenberechnung zeigt, dass diese Überlegung korrekt ist und zum identischen Flächeninhalt von 3848,451 mm² führt.
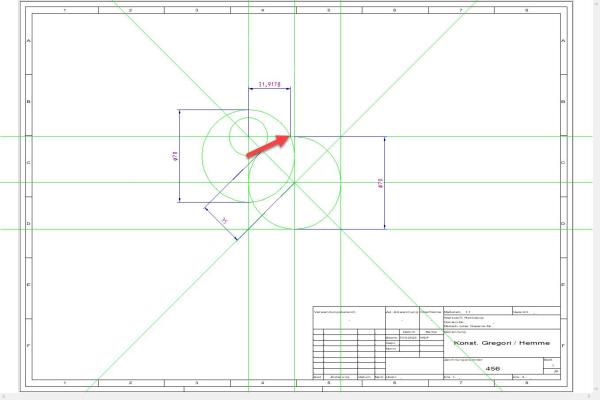
5. Hilfskreis 2 mit Durchmesser D70 einzeichnen (Der rote Pfeil zeigt auf einen wichtigen Schnittpunkt)
Mit einem Ergebnis von 62,02055 Millimeter für die Strecke s des Quadrats ist diese Lösung erstaunlich nahe am errechneten Wert von 62,03588. Der Unterschied beträgt lediglich 0,01533 Millimeter!
Hans Hampel hat mit seiner jahrelangen Beschäftigung zu diesem Thema bereits 2019 eine interessante Lösung gefunden, die ebenfalls sehr einfach ausfällt und eine ähnlich genaue Annäherung an die tatsächliche Größe des Quadrats erlaubt.
Konstruktion eines flächengleichen Quadrats aus einem gegebenen Kreis nach Hans Hampl:
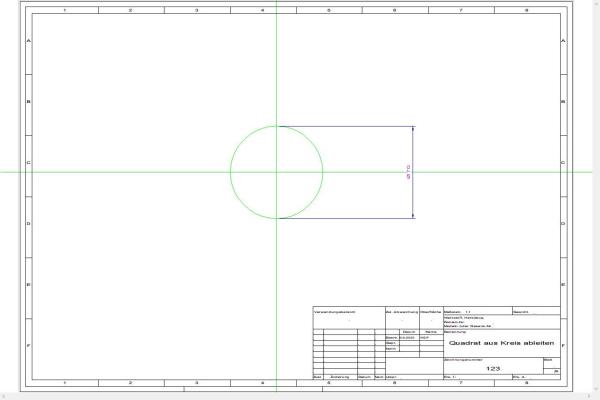
1. Hilfslinien und Kreis Durchmesser 70 einzeichnen
Auch dieses Resultat zeigt, dass es problemlos mittels eines CAD-Systems und erst recht mit Lineal und Zirkel möglich ist – ausgehend von einem Kreis – konstruktiv ein Quadrat zu erstellen, das nahezu perfekt über die gleiche Fläche wie der Kreis verfügt. Es gibt bei der Konstruktion von Hans Hampel ebenfalls keine großen Abweichungen zum berechneten Wert. Diese beträgt lediglich: 62,03588 (errechneter Wert) – 61.993266 (konstruierter Wert) = 0,042614 Millimeter!
Festzuhalten ist somit, dass die lange angenommene Unmöglichkeit, mittels Zirkel und Lineal aus einem Kreis ein flächengleiches Quadrat zu erstellen, nahezu widerlegt ist, denn ein Fehler von weniger als 0,015 Millimeter (Gregori/Hemme) beziehungsweise 0,043 Millimeter (Hampl) könnte mit diesen Mitteln überhaupt nicht erkannt werden. Somit ist die Aussage, dass die Quadratur des Kreises nicht möglich ist, aufgrund der gezeigten Lösungen als widerlegt anzusehen, da die mit diesen Lösungen erreichte Genauigkeit für viele konstruktive Aufgaben völlig ausreichend ist. Ganz abgesehen davon, dass moderne CAD-Systeme das Erstellen technischer Zeichnungen mit Lineal und Zirkel schon lange in die Geschichtsbücher verbannt haben.
Vertiefende Quellen:
Die Nebra-Scheibe ein Uhrenteil?
Die Quadratur des Kreises (Wikipedia-Artikel)





















